EMMP

Abstract

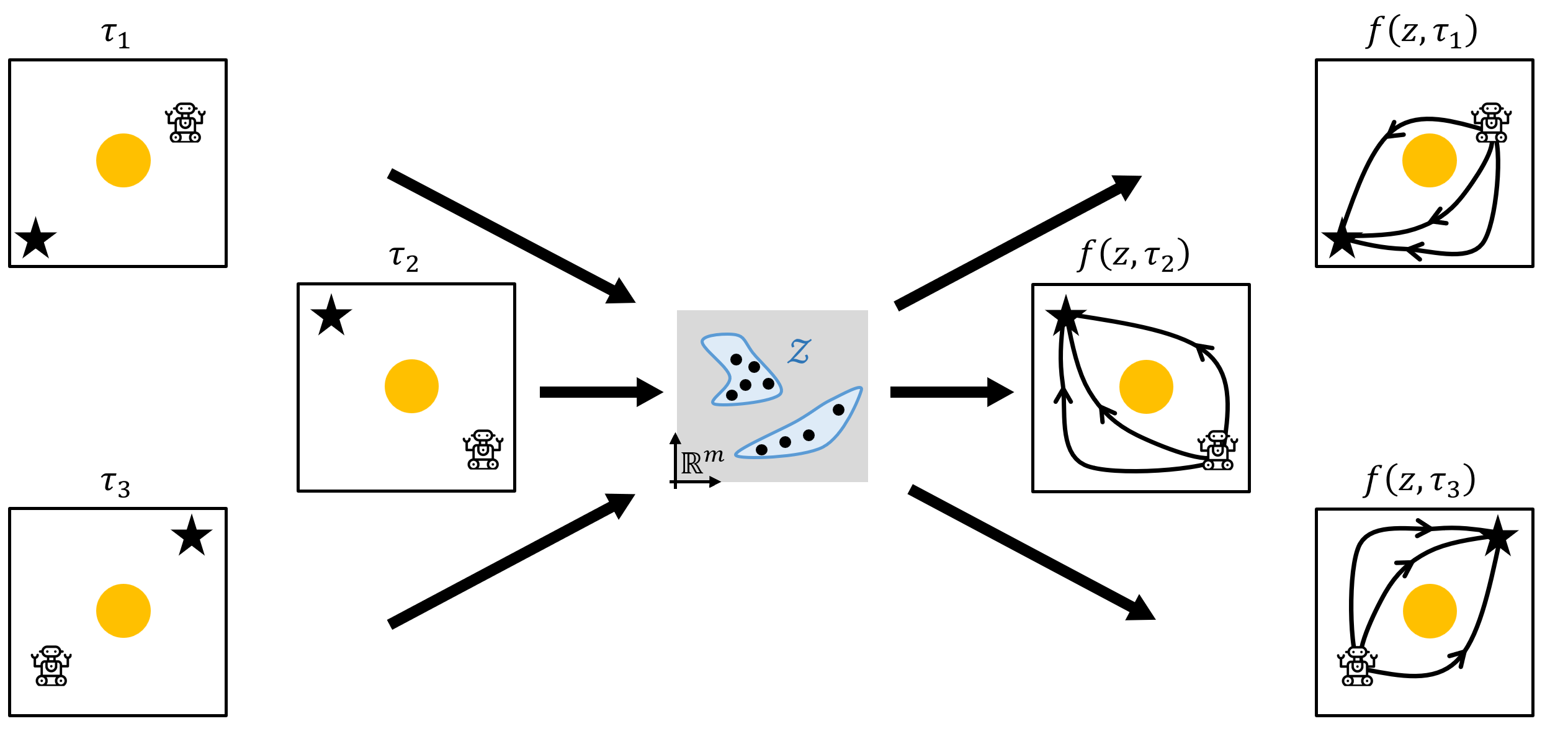
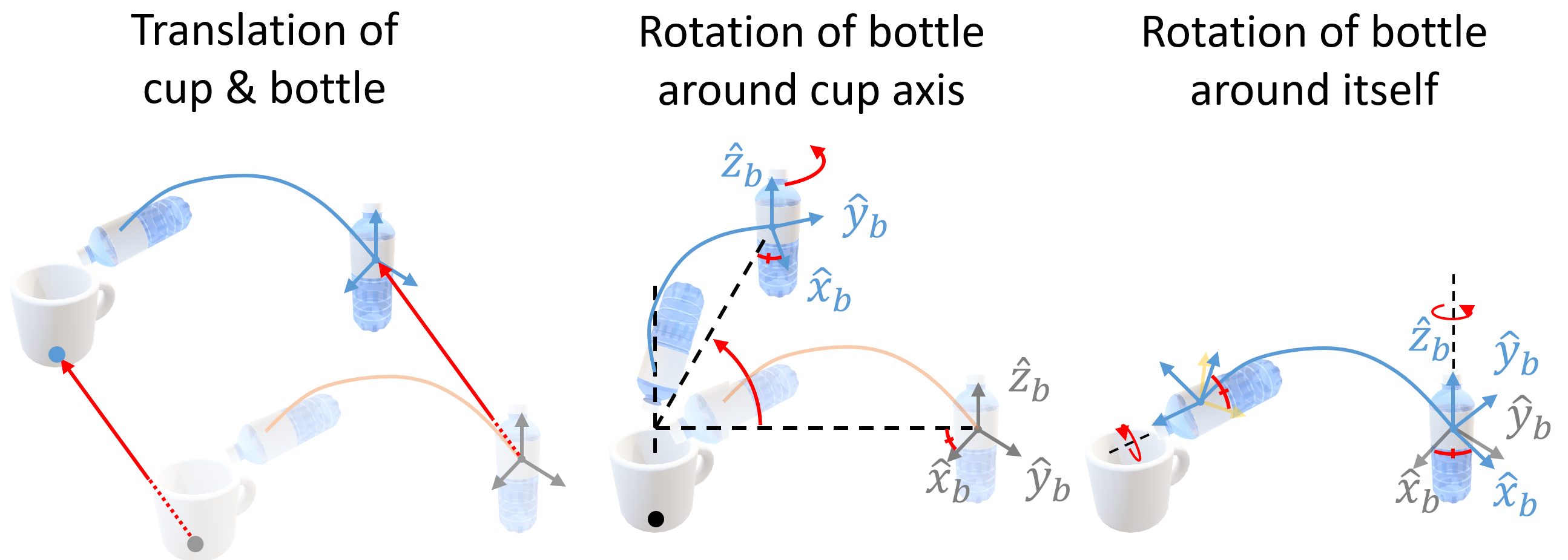
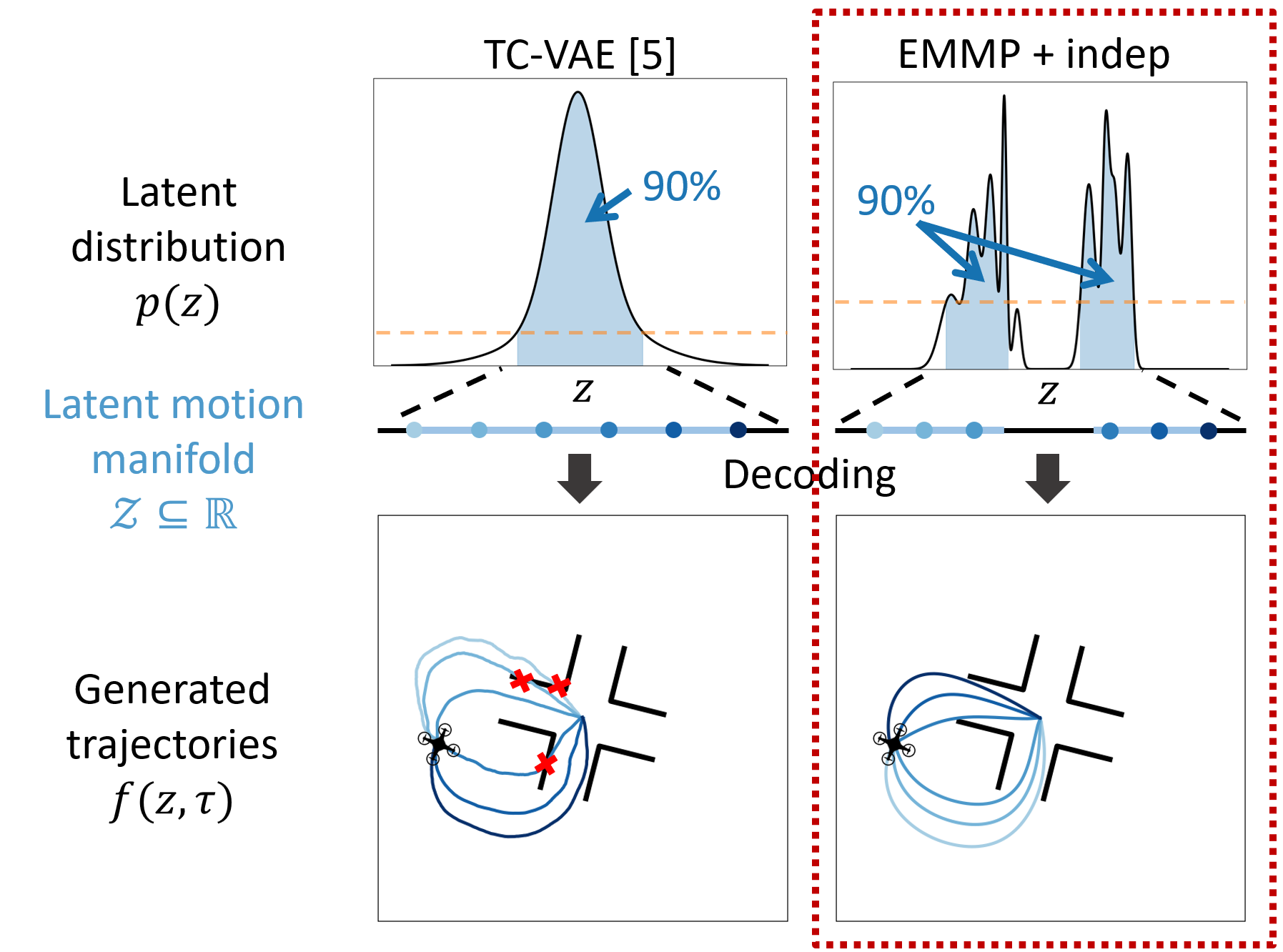
Existing movement primitive models for the most part focus on representing and generating a single trajectory for a given task, limiting their adaptability to situations in which unforeseen obstacles or new constraints may arise. In this work we propose Motion Manifold Primitives (MMP), a movement primitive paradigm that encodes and generates, for a given task, a continuous manifold of trajectories each of which can achieve the given task. To address the challenge of learning each motion manifold from a limited amount of data, we exploit inherent symmetries in the robot task by constructing motion manifold primitives that are equivariant with respect to given symmetry groups. Under the assumption that each of the MMPs can be smoothly deformed into each other, an autoencoder framework is developed to encode the MMPs and also generate solution trajectories. Experiments involving synthetic and real-robot examples demonstrate that our method outperforms existing manifold primitive methods by significant margins. Code is available at https://github.com/dlsfldl/EMMP-public.

Latent Space Modulation

Trajectory Sampling

Video

Motion Manifold Primitives (MMP)

Under the assumption that all motion manifolds can be smoothly defromed into each other, our model learns a shared latent space of all task parameters. Then, our model maps a latent value \(z\) and a task parameter \(\tau\) into a reconstructed trajectory \(\hat{x}\).

Inherent symmetry within tasks

There exist inherent symmetries within robot tasks, such as rotational symmetry or translational symmetry.

Equivariant Motion Manifold Primitives (EMMP)

We propose Equivariant Motion Manifold Primitives (EMMP) that are equivariant with respect to the inherent symmetries within tasks.

Experiment Results

1. Navigation in 2D

2. Water Pouring Motion in SE(3)

Supplementary Video

Citation


      @inproceedings{lee2023equivariant,
        title={Equivariant motion manifold primitives},
        author={Lee, Byeongho and Lee, Yonghyeon and Kim, Seungyeon and Son, MinJun and Park, Frank C},
        booktitle={7th Annual Conference on Robot Learning},
        year={2023}
      }

Equivariant Motion Manifold Primitives

TL;DR: This paper propose a new family of highly adaptable primitive models, Equivariant Motion Manifold Primitives (EMMP), which consider inherent symmetry in the robot tasks.